(7,141 - 7,160 of 10,082)
Pages
-
-
Title
-
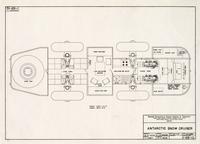
Antarctic Snow Cruiser
-
Date
-
1939-08-09
-
Description
-
Overhead plan for The Snow Cruiser, designed and checked by Dr. Thomas C. Poulter, drawn by C.E. Hammett, and traced by E.J. Loutzenheiser....
Show moreOverhead plan for The Snow Cruiser, designed and checked by Dr. Thomas C. Poulter, drawn by C.E. Hammett, and traced by E.J. Loutzenheiser. The Snow Cruiser was designed by Armour Research Foundation Scientific Director Thomas C. Poulter, constructed by ARF, and taken on Richard Byrd's third Antarctic expedition.
Show less
-
Collection
-
Henry T. Heald, University President's papers, 1920-1953
-

-
Title
-
Antarctic Snow Cruiser
-
Date
-
1939-08-09
-
Description
-
Plan for The Snow Cruiser, designed and checked by Dr. Thomas C. Poulter, drawn by C.E. Hammett, and traced by E.J. Loutzenheiser. The Snow...
Show morePlan for The Snow Cruiser, designed and checked by Dr. Thomas C. Poulter, drawn by C.E. Hammett, and traced by E.J. Loutzenheiser. The Snow Cruiser was designed by Armour Research Foundation Scientific Director Thomas C. Poulter, constructed by ARF, and taken on Richard Byrd's third Antarctic expedition.
Show less
-
Collection
-
Henry T. Heald, University President's papers, 1920-1953
-

-
Title
-
Binary hidden Markov models and varieties, AS2012 Special Volume, part 2: This issue includes a second series of papers from talks, posters and collaborations resulting from and
inspired by the Algebraic Statistics in the Alleghenies Conference at Penn State, which took place in July
2012.
-
Date
-
2013, 2013
-
Description
-
This paper closely examines HMMs in which all the hidden random variables are...
Show moreThis paper closely examines HMMs in which all the hidden random variables are
binary. Its main contributions are (1) a birational parametrization for every such HMM, with an
explicit inverse for recovering the hidden parameters in terms of observables, (2) a semialgebraic
model membership test for every such HMM, and (3) minimal dening equations for the 4-node
fully binary model, comprising 21 quadrics and 29 cubics, which were computed using Grobner
bases in the cumulant coordinates of Sturmfels and Zwiernik. The new model parameters in (1) are
rationally identiable in the sense of Sullivant, Garcia-Puente, and Spielvogel, and each model's
Zariski closure is therefore a rational projective variety of dimension 5. Grobner basis computations
for the model and its graph are found to be considerably faster using these parameters. In the
case of two hidden states, item (2) supersedes a previous algorithm of Schonhuth which is only
generically dened, and the dening equations (3) yield new invariants for HMMs of all lengths
4. Such invariants have been used successfully in model selection problems in phylogenetics, and
one can hope for similar applications in the case of HMMs.
Show less
-
Collection
-
Journal of Algebraic Statistics
-

-
Title
-
On Polyhedral Approximations of Polytopes for Learning Bayesian Networks, AS2012 Special Volume, part 2: This issue includes a second series of papers from talks, posters and collaborations resulting from and
inspired by the Algebraic Statistics in the Alleghenies Conference at Penn State, which took place in July
2012.
-
Date
-
2013, 2013
-
Description
-
The motivation for this paper is the geometric approach to statistical learning Bayesiannetwork (BN) structures. We review three vector...
Show moreThe motivation for this paper is the geometric approach to statistical learning Bayesiannetwork (BN) structures. We review three vector encodings of BN structures. The first one has been used by Jaakkola et al. [9] and also by Cussens [4], the other two use special integral vectors formerly introduced, called imsets [18, 20]. The topic is the comparison of outer polyhedral approximations of the corresponding polytopes. We show how to transform the inequalities suggested by Jaakkola et al. [9] into the framework of imsets. The result of our comparison is the observation that the implicit polyhedral approximation of the standard imset polytope suggested in [21] gives a tighter approximation than the (transformed) explicit polyhedral approximation from [9]. As a consequence, we confirm a conjecture from [21] that the above-mentioned implicit polyhedral approximation of the standard imset polytope is an LP relaxation of that polytope. In the end, we review recent attempts to apply the methods of integer programming to learning BN structures and discuss the task of finding suitable explicit LP relaxation in the imset-based approach.
Show less
-
Collection
-
Journal of Algebraic Statistics
Pages